Proof of the formulae for s.h.m. (1)

There are two alternative proofs. We will give the mathematical one first because it is the more satisfactory of the two.

Simple harmonic motion is defined by the equation: acceleration = -ω²x or dv/dt = -ω²x

Therefore: v dv/dx = - ω²x and when integrated this becomes v²/2 = -ω²x²/2 + C

Using the limits V = 0 when x = r, and v = rω when x = 0, gives C = ω²r²/2.
Therefore:



Note the +/- sign, showing that the velocity can be in either direction about the midpoint.

Therefore   v = dx/dt = +/- ωv (r² – x²) which when integrated becomes



with the limits x = +/- r when t = π/2ω or 3π/2ω and x = 0 when t = 0, π/ω or 2θ/ω

Proof of the formulae for s.h.m. (2)

The next proof is slightly less mathematical, and uses the projection on a diameter of a circle of the motion of a point P round the circle. Let the velocity of the particle round that circle be U and the velocity of the projection on AB be v (Figure 1). We wish to show that the motion of the projection of P on AB is s.h.m.

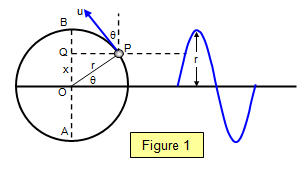
The displacement (x) of the projection of P from O along AB is given by

x = r sinθ = r sin ωt

Consider the component of velocity of P parallel to AB: this will be the velocity of the projection of P on AB.



Component parallel to AB = u cos ωt = rω cos ωt = rω(1 – sin²ωt)^1/2 = rω(1-x²/r²)^1/2.

Therefore:



Now the acceleration of P will be towards the centre of the circle and therefore its component parallel to AB will be:
acceleration = -ω²r sin ωt = - ω²x

This is s.h.m., since we have shown that the acceleration of Q is directed towards O and proportional to OQ.

schoolphysics SHM and circular motion

To see an animation of the connection between shm and circular motion click on the animation link.